De Aristóteles a Einstein
Una revisión breve de los marcos teóricos fundamentales para el análisis del movimiento como sujeto de estudio de la física.
El inicio de esta historia se remonta al siglo IV a.e.c., época de la Academia de Platón y El Liceo de Aristóteles, quien da nombre al primero de estos modelos. La física de Aristóteles postulaba dos principios fundamentales: que los cuerpos caen a velocidad constante y que los objetos más pesados caen más rápido que los livianos. Además, proponía que los cuerpos pesados encuentran su lugar natural en el centro del universo que, al amparo de una lógica geocéntrica, es el centro de la Tierra. Por otro lado, los cuerpos livianos, como los gases, hallaban su lugar natural en el cielo.
Uno de los aspectos principales en que fallaba el modelo aristotélico era que ponía el movimiento en el medio en lugar de en el objeto. Esta asunción producía un problema lógico grave: si el movimiento se produce en el medio y no en el objeto, ¿cómo se puede explicar el movimiento de los cuerpos en el vacío? A pesar de este y otros errores, la física aristotélica fue de gran importancia como teoría del movimiento —hay que pensar que se aceptó desde la época en que vivió su autor hasta el siglo XVII.
Muchos años después de Aristóteles, apareció Galileo.
Galileo vivió en una época (segunda mitad del siglo XVI y primera mitad del siglo XVII) en que la teoría de movimiento más ampliamente aceptada seguía siendo la de Aristóteles, propuesta más de un milenio antes. A pesar de que podríamos decir que Galileo no desarrolló una teoría de movimiento completa, sí es cierto que a través de ciertos experimentos, el italiano puso en duda algunos de los principios del modelo vigente, como por ejemplo la manera en que estaba definida la trayectoria de una bala de cañón.
Las balas de cañón no seguían una línea recta hasta agotar el ímpetu que las impulsaba y luego caían directo al suelo como creía Aristóteles, sino que recorrían la trayectoria de un arco parabólico subiendo cada vez más lento hasta alcanzar una altura máxima y luego comenzaban a descender cada vez más rápido —por ponerlo en términos simples.
A través de otro experimento, Galileo observó que, a diferencia de lo que pensaba Aristóteles y siempre que se despreciara el efecto del roce producido por el aire, todos los cuerpos caían con la misma aceleración independiente de su masa. En lo particular, la comprensión de este fenómeno me resultó mucho más sencilla al analizar la fórmula —aunque newtoniana— que se usa para determinar el tiempo que demora un objeto en caída libre, ya que el tiempo t no depende de la masa del cuerpo:
Otro golpe indirecto al pensamiento aristotélico también vino de la mano —o mejor dicho de la mente— de Galileo, cuando este descubrió varios pequeños satélites o lunas orbitando alrededor de Júpiter. Este descubrimiento probó que no todos los cuerpos celestes tenían que orbitar en torno a la Tierra tal como Aristóteles y Ptolomeo habían pensado. No solo Galileo, sino también Kepler, pasaron a apoyar el modelo heliocéntrico en detrimento del modelo geocéntrico, el que había recibido el golpe de gracia.
No mucho después, surge un personaje reconocido como una de las mentes más brillantes del periodo final de la Ilustración que se conoce como la Era de la Razón: Isaac Newton. La historia nos cuenta que luego de que en 1665 los estudiantes del Trinity College —donde estudiaba— enviado a casa para evitar la última epidemia de peste bubónica en Inglaterra, y con tan solo 22 años, este genio habría inventado sus desarrollos del cálculo diferencial e integral, los que le habrían permitido formular las Leyes Fundamentales de la Naturaleza, como la Ley de la Gravedad y las Leyes de la Mecánica.
La ley de la gravitación universal, matematizada en 1687 por Newton, es una teoría respecto de cómo se mueven los cuerpos en el espacio y el tiempo. Postula que cada cuerpo en el Universo es atraído hacia cada uno de los demás por una fuerza cuya magnitud es proporcional a la masa del cuerpo e inversamente proporcional al cuadrado de la distancia entre ellos. Esto quiere decir que la fuerza es más intensa cuanto más masivos son los objetos y cuanto más próximos se encuentran. Matemáticamente se ve así:
Ese mismo año —y en el mismo libro: sus Principia Mathematica— incluiría lo que hoy se conoce como leyes del movimiento o de la mecánica. Estas tres leyes más la incorporación del concepto de sistema de referencia, pusieron fin a la idea de una posición absoluta en el espacio, pues todo depende de la posición del observador.
La primera ley de Newton o ley de inercia señala que cuando sobre un cuerpo no actúa ninguna fuerza, este seguirá moviéndose en una línea recta a velocidad constante. Puesto de otra manera, cada cuerpo permanece en su estado de reposo o de movimiento uniforme en línea recta, a menos que su estado cambie producto de la aplicación de fuerzas sobre él. Esta ley es la que permite que en la situación representada en la figura a continuación la moneda caiga dentro del vaso al retirar la lámina lo suficientemente rápido —lo que está quieto se tiende a quedar quieto.
La segunda ley de Newton o ley fundamental de la dinámica establece que un cuerpo acelerará o cambiará su velocidad de manera proporcional al tamaño de la fuerza que se ejerza sobre él y en la dirección de la recta en que se aplica dicha fuerza. En la situación de la figura, dada una misma fuerza, la aceleración producida sobre una masa será inversamente proporcional a su magnitud. Es decir, si se aplica una cierta fuerza a un objeto de masa pequeña se producirá una gran aceleración, mientras que la misma se aplica a un objeto de masa grande la aceleración será pequeña.
La tercera ley de Newton o principio de acción y reacción —que me recuerda la reiterativa frase del director Rachin "Action, réaction" en la película Les choristes— establece que siempre que un objeto ejerce una fuerza sobre un segundo objeto, este ejerce una fuerza de igual magnitud y dirección, pero en sentido opuesto sobre el primero. En otras palabras, a cada acción se opone siempre una reacción igual pero en contra.
Finalmente, llegamos a Einstein. A don Albert se le conoce un solo error en su vida como científico: la reincorporación de la constante cosmológica en sus ecuaciones de campo para que los resultados concordaran con su creencia de que el universo era estático. Hubble no tardó en demostrar que el universo muy lejos de estar quieto, se encontraba en expansión acelerada.
El master opus de Einstein es sin lugar a dudas la teoría de la relatividad, que partió con un modelo restringido que no incluía la gravedad —la relatividad especial— pero que no tardó en ampliar a uno que sí lo hacía —la relatividad general. En este último consiguió que todos los observadores independiente de sus velocidades relativas calcularan el mismo valor para g.
Lo que nos ocupa en este recuento es la teoría de la relatividad general. Tan pronto como Einstein se dio cuenta de que la teoría de la relatividad estaba incompleta porque la aceleración resultaba problemática y no había cómo explicar la gravedad, llegó a la idea que marcaría un punto de inflexión. Al notar que un hombre en caída libre no siente su peso había dado el primer paso hacia lo que hoy se conoce como principio de equivalencia, un elemento fundante de la teoría de la relatividad general.
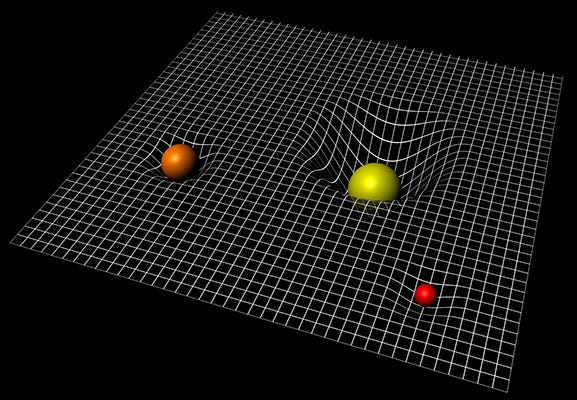
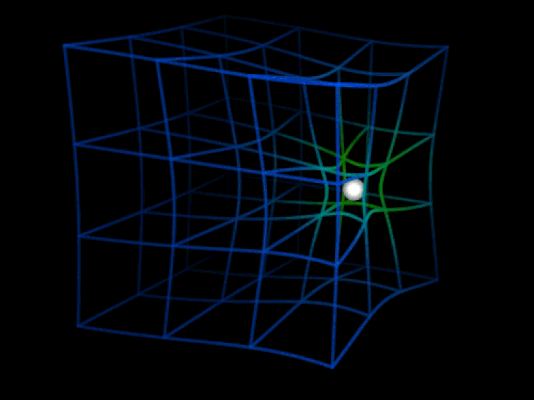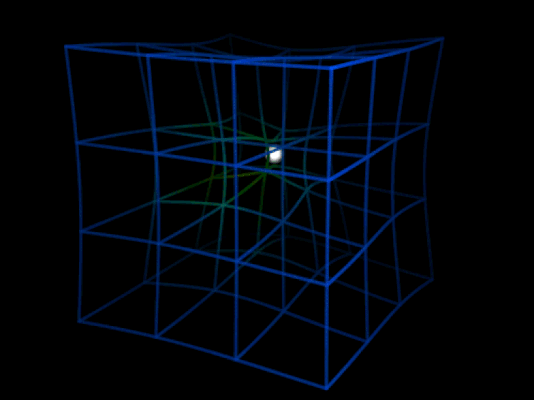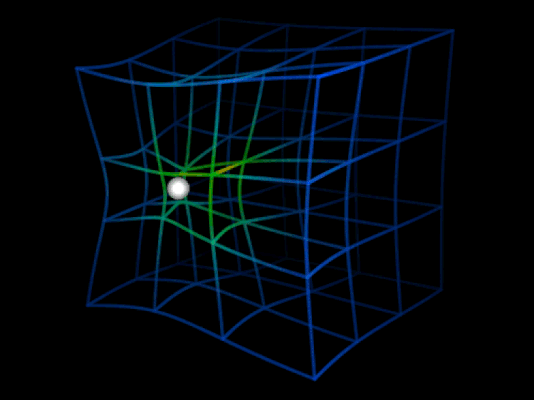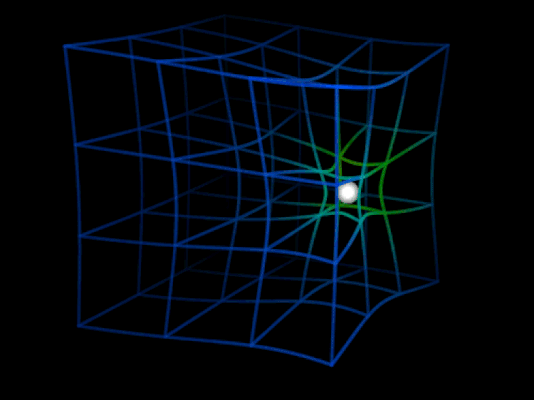
El principio de equivalencia postula que la masa gravitacional y la masa inercial son equvialentes. En otras palabras, gravedad y aceleración son lo mismo. Como la caída libre es un movimiento inercial, la conclusión era clara: el espacio debía estar curvado. Es así como, según la relatividad general, la tela o entramado del espacio-tiempo (una 4-variedad usada en cosmología para analizar la estructura del universo que, por cierto, podemos abordar en otro escrito) se curva en presencia de masa-energía —dos cantidades que también son equivalentes— hundiéndose como una tela bajo la fuerza ejercida por un objeto masivo que se apoya encima.
Pero el asunto no se detiene ahí. John Wheeler, observando las ecuaciones de campo de Einstein —las mismas que predicen la existencia de agujeros negros— interpretaría más tarde que, así como la materia-energía curva el espacio-tiempo, a su vez la curvatura del espacio-tiempo determina la manera en que la materia-energía se mueve por el espacio.
Tal como se observa en la animación superior, cuando una masa se mueve por una región curvada del espacio, experimenta una aceleración debida a esta curvatura, pero además experimenta un efecto adicional producido porque la curvatura del espacio cambia a su paso.
Lo aquí expuesto hace parecer que estos modelos hubiesen ido surgiendo casi por arte de magia y que cada uno de sus exponentes hubiese notado algo demasiado obvio como para que sus antecesores no lo tuvieran en cuenta, pero la verdad es que el desarrollo completo de estas teorías es mucho más larga y enrevesada. Dos razones me han impedido ahondar más: en primer lugar, mi reconocida ignorancia de otros aspectos que puedan resultar tanto o más importantes y segundo, mi empeño por respetar el adjetivo que comienza el título de este recuento histórico. El trabajo de investigación y la posibilidad de profundizar en el aprendizaje queda en manos del lector curioso (y en mis futuros intentos de poner algo por escrito).